TL;DR
- The huggingface implements DynamicNTK RoPE with a potential inconsistency problem in rotation base between keys
- Current perplexity evaluation cannot faithfully reflect whether the inconsistency problem can harm the perplexity.
- The inconsistency in DynamicNTK RoPE can be fixed with
use_cache=False, at the cost of speed.
Weeks ago, u/emozilla proposed an improvement on NTK-Aware RoPE in this post, later named DynamicNTKScalingRotaryEmbedding.
The main idea behind Dynamic NTK is to use a scaling factor relative to the present decoding sequence length to improve the base functionality, which means that if we represent the base of NTKRoPE as:
\[\theta_j = (\alpha^{dim/dim-2} \times 10000)^{-2j/dim}\]
\(\alpha\) is the scale of the max sequence length we extend by interpolation w.r.t. the pretrained max sequence length.
Then the Dynamic NTK is to scale up the \(\alpha\) as:
\[\alpha_{\text{dynamicNTK}} = \alpha * \dfrac{\text{max\_seq + scale * (seq - max\_seq)}}{ \text{max\_seq}}\]
\(\text{max\_seq}\) is max sequence length of pretrained model, for example, for LLaMA-1-7B, \(\text{ max\_seq } = 2048\); \(\text{seq}\) is the current sequence length;
According to the equation, we can see that as the sequence length keeps growing, the scaling factor continues to increase as well, which means the larger the base, the slower the rotation speed along all dimensions.
However, here is a possible rotation inconsistency problem that could result in a relative position mismatch between the key and query as the sequence length growing.
Inconsistency Problem
Let’s denote:
key_states = self.k_proj(hidden_states)
value_states = self.v_proj(hidden_states)
when the decoder tries to generate the 100th token, \(\text{seq}=100\) and the key_states at the index \(j\) is rotated based on a base
\[\alpha_1 = \alpha * \dfrac{\text{max\_seq} + \text{scale} * (100 - \text{max\_seq)}}{\text{max\_seq}}\]
Similarly, for the 200th token, \(\text{seq}=200\) and the key_states at index \(j\) is rotated based on a base
\[\alpha_2 = \alpha * \dfrac{\text{max\_seq} + \text{scale} * (200 - \text{max\_seq)}}{\text{max\_seq}}\]
Here we can clearly see that these two \(\alpha\) are different.
Since we use key-value caches to speed up generation, the multiplication between the key and the query can be written as:
\[\begin{equation} \text{Q}\text{K}^ T = [r(k_0, \alpha_0), r(k_1, \alpha_1), r(k_2, \alpha_2)] * r(q, \alpha_2) \end{equation}\]
\(r(k, \alpha)\): apply RoPE on the key with a rotation base \(\alpha\)
Here, we can clearly see there is an inconsistent rotation base between the keys and queries.
From my understanding, a consistent rotation between keys and queries should be like this:
Firstly,
\[\begin{equation} \text{Q}\text{K}^ T= [r(k_0, \alpha_1), r(k_1, \alpha_1)] * r(q, \alpha_1) \end{equation}\]
when seq length increases
\[\begin{equation} \text{Q}\text{K}^ T = [r(k_0, \alpha_2), r(k_1, \alpha_2), r(k_2, \alpha_2)] * r(q, \alpha_2) \end{equation}\]
The relative position introduced by RoPE between all keys and queries in eq3 looks more reasonable when compared to eq1.
I believe that, from a mathematical perspective, keeping consistency in the rotation base could potentially enhance the language model’s ability to learn relative positions more effectively. My intuition suggests that this consistency might offer advantages in capturing relative position information.
The Gap between Perplexity Evaluation and Generation
There is actually a gap between how we compute perplexity and how the LLM actually generates tokens.
During the decoding process in every layer of decoders, the key_states and query_states are computed from the hidden features. Then, they are rotated based on a fixed seq_len. However, in the decoding phase, LLM usually reuses previous cached keys which are rotated based on factors related to seq_len to save memory. As the seq_Len keeps increasing, inconsistency arises between keys and queries.
Therefore, our current evaluation methods are unable to accurately reflect whether such inconsistency in Dynamic NTK RoPE can harm perplexity or not. In other words, the way how we currently compute perplexity is more like we keep the rotation base consistent.
To mitigate such a gap between perplexity evaluation and inference, I modified the codes about applying the rotary embedding on keys and queries in this repo and do simple experiments on Llama1-7B.
After modification, the perplexity is computed like this:
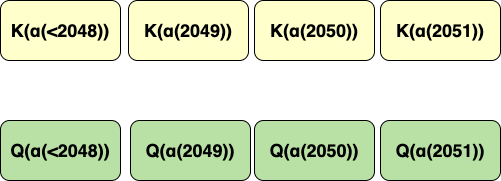
\(K(\alpha(x))\) means, the key is rotated by a rotation matrix whose base is a function of \(n\)
Here are some results:
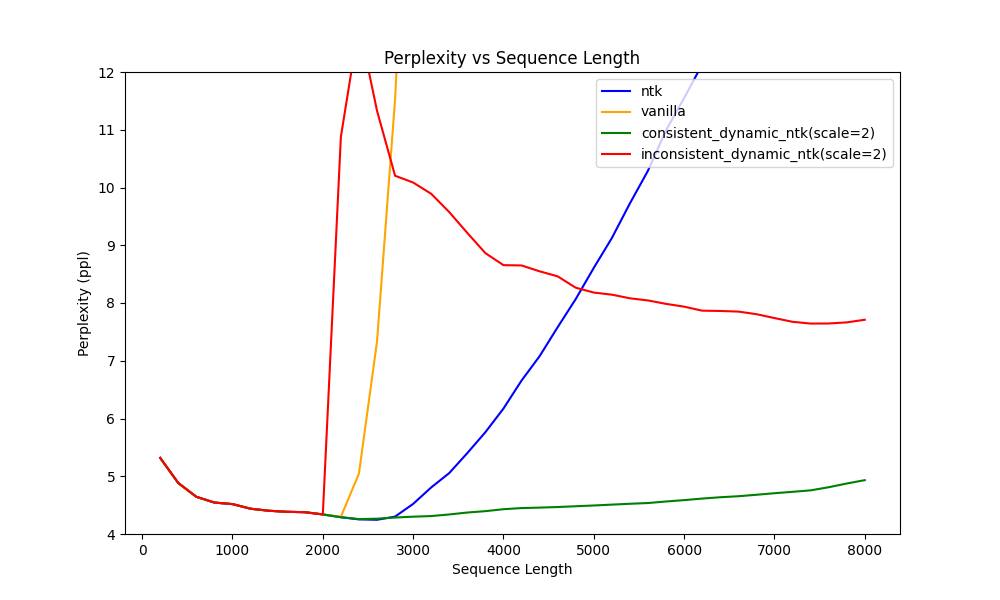
Figure 1, Perplexity value on Llama1-7B, a 2k max sequence length model, values above 12.0 are cut off for concise; Vanilla: RoPE w/o any interpolation; NTK: DynamicNTK when scale=1; Consistent DynamicNTK: keep rotation base between keys consistent, current huggingface implementations; Inconsistent DynamicNTK: keep rotation base between keys inconsistent w.r.t context length;
We can see from Figure 1 that when keeping the rotation base between keys inconsistent w.r.t context length, the perplexity significantly increases, indicating DynamicNTK harms the performances. This finding might initially seem counterintuitive.
However, as the sequence length continues to grow, we can notice a gradual reduction in perplexity for inconsistent Dynamic NTKScale RoPE. Interestingly, the inconsistent Dynamic NTKScale RoPE outperforms the NTKScale RoPE in terms of perplexity when the sequence length exceeds \(5,000\).
This may suggest why we tend to ignore the inconsistency in the rotation because it does benefit a longer context beyond a certain sequence length. Please check Table 1 for more detailed ppl value.
| Lenth |
Consistent Dynamic NTKScale PPL |
Inconsistent Dynamic NTKScale PPL |
NTKScale PPL |
| 2800 |
4.285102386474609 |
10.203343925476075 |
4.301338438987732 |
| 3600 |
4.371902356147766 |
9.213108296394347 |
5.401671919822693 |
| 5600 |
4.536222472190857 |
8.04413757801056 |
10.291163015365601 |
| 7200 |
4.7303602981567385 |
7.674421100616455 |
15.359781618118285 |
| 8000 |
4.932255864143372 |
7.7100021314620975 |
15.884212293624877 |
Table 1: PPL Value of Different NTKScale Methods
Latency of consistent vs inconsistent dynamic scaling
The main difference between my implementations and huggingface’s is as follows:
In the former approach, all keys are cached before RoPE is applied to a length-increasing key_states list. The latter one applies RoPE only to a single key_state. Therefore, we just need to confirm whether applying RoPE on a length-increasing key_states list will take more time than applying it to a single key_state.
Here is the exec time of apply_rotary_pos_emb in consistent DynamicNTKScale RoPE on LLaMA-7B (32 layers)
| seq_length |
exec time (ms) |
seq_length |
exec time (ms) |
| 16 |
56.32 |
528 |
206.08 |
| 32 |
44.48 |
544 |
194.88 |
| 48 |
39.68 |
560 |
197.44 |
| 64 |
30.72 |
576 |
215.36 |
| 80 |
43.84 |
592 |
207.04 |
| 96 |
25.28 |
608 |
211.52 |
| 112 |
26.24 |
624 |
220.16 |
| 128 |
24.32 |
640 |
227.84 |
| 144 |
35.2 |
656 |
245.76 |
| 160 |
26.88 |
672 |
238.4 |
| 176 |
71.68 |
688 |
248.64 |
| 192 |
65.6 |
704 |
246.72 |
| 208 |
95.04 |
720 |
270.08 |
| 432 |
161.28 |
944 |
356.48 |
| 448 |
164.16 |
960 |
367.36 |
| 464 |
172.8 |
976 |
354.56 |
| 480 |
177.92 |
992 |
365.12 |
| 496 |
178.88 |
1008 |
407.68 |
You can find the exec time eval script here:
According to the table above: The throughput of consistent is impaired compared to that of dynamic’s.
Limitation
In fact, I haven’t found any practical downstream tasks where the consistent RoPE can bring significant performance improvement. The only advantage convinces me to replace it is its potential to achieve better perplexity scores on very long contexts. However, considering that it trades consistency with speed, it is less necessary to correct this inconsistency in the RoPE. Speed does matter more than correctness :)
Still, my experiments have some limitations. I only test it on one dataset with limited samples. I hope my finds can be helpful to you. If there is any mistake in my codes or experiments, I’ll appreciate it if you could kindly point it out. Please feel free to raise an issue in the repo as well.